이분 탐색(Binary Search), 어떨 때 적용할까?

이분(이진) 탐색이란?

적용

연습 문제

🔗 프로그래머스, 예산

🔗 프로그래머스, 입국심사

⍞ Reference

이분(이진) 탐색이란?

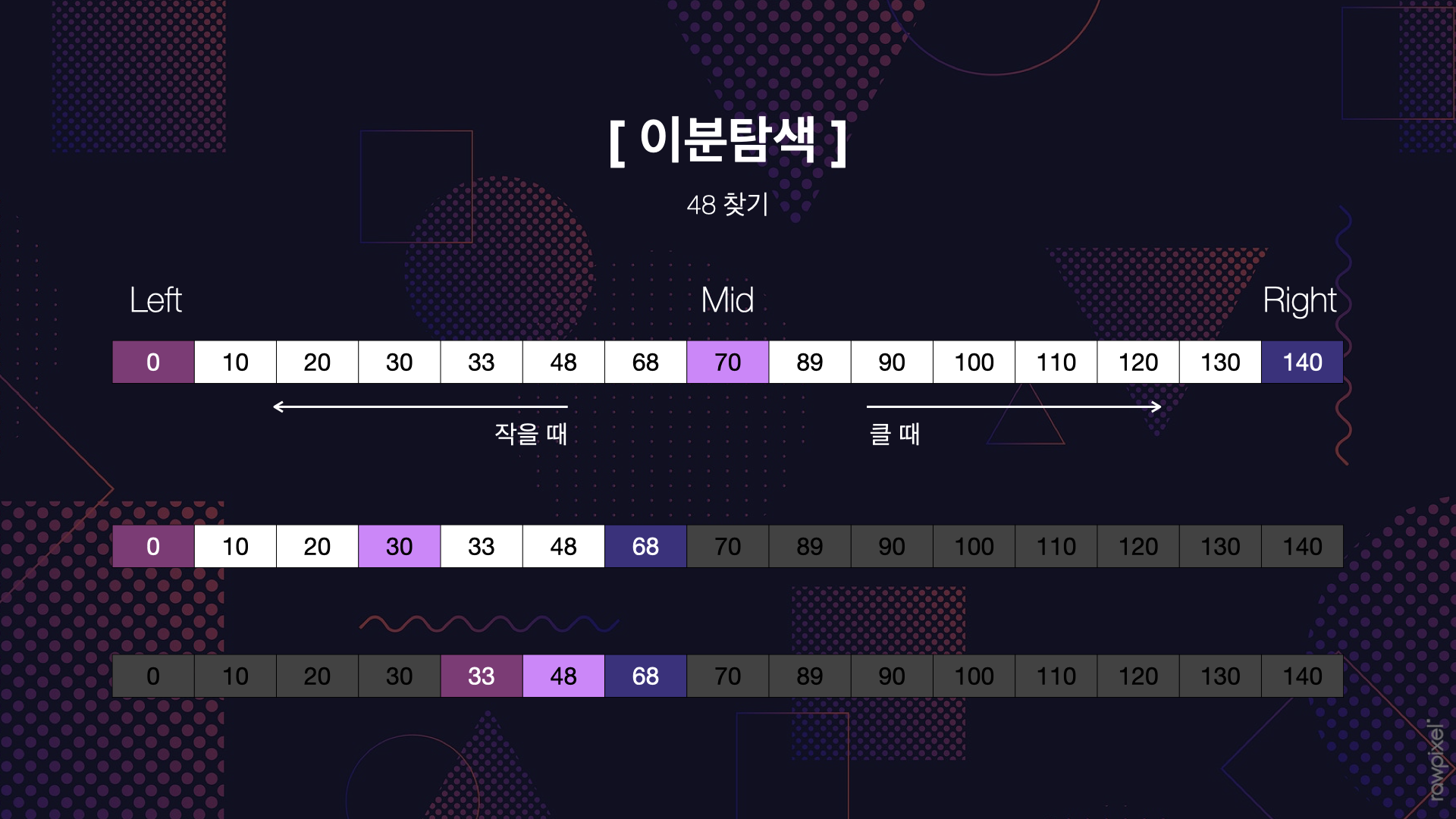
찾고자 하는 값을 검색할 때,
범위의 가운데 값을 검사하여 원하는 값이 나올 때까지 반씩 줄여나가며 찾는다.

사전을 찾을 때 그냥 한번 펼쳐서 찾는 단어가 없으면 위치에 따라 앞쪽을 찾거나 뒤쪽을 찾고
이 과정을 찾을 때까지 반복하는 것을 생각하면 된다.

• 속도 : O(log N)

  🤖

  O(log N)의 위력이 감이 잘 안 온다면,
  4,294,967,296개(약 43억 개)의 원소가 있는 리스트에서 원하는 특정 값을 찾아낼 때 최악의 탐색 깊이(찾는 값이 없는 경우)는 딱 32회이다. 그러나 순차 탐색의 최악의 경우는 4,294,967,296회이다. 저게 0부터 순서대로 숫자가 들어있는 리스트라고 할 때 순차 탐색이 이진 탐색보다 빠른 지점은 32까지. 33부터 그 나머지 구간에서는 이진 탐색이 순차 탐색보다 빠르다. 33회의 비교 시에는 약 86억 개의 자료를 탐색할 수 있다. 우주에 존재하는 모든 원자 개수만큼의 원소를 가지는 리스트를 주어줘도 약 120회 정도만 비교하면 원하는 값을 찾을 수 있다.
  - 나무위키, 이진 탐색

 

이론적으로는 이해하기도 쉽고 아주 단순한 개념이다.

하지만 막상 문제로 처음 마주친다면 어디에 어떻게 이분 탐색을 적용해야 할지 헷갈린다.

적용

1. 정렬된 자료

이분 문제를 처음 접했을 때, 대상을 선정하는데에 있어서 이 부분 때문에 헷갈렸던 것 같다.
순서대로 값이 놓여 있어야 한다는 것이지 뒤죽박죽되어있는 것을 놓고 정렬해야 한다는 생각을 버리자.

보통 범위를 두고 조건에 맞는 범위를 찾아 조정해 나가면서 사용하게 된다.
→ 범위라는 것은 숫자가 순서대로 나열되어 있고, 거기에서 최소-최대를 뜻하니 정렬된 자료라고 할 수 있다.

 

2. 최소를 구하시오 or 최대를 구하시오

→ 조건에 맞는 답은 여러 개이지만, 그중 최소/최대를 구해야 할 때 유용하게 사용된다.

 

연습 문제

🔗 프로그래머스, 예산

1. 모든 요청이 배정될 수 있는 경우에는 요청한 금액을 그대로 배정합니다.
2. 모든 요청이 배정될 수 없는 경우에는 특정한 정수 상한액을 계산하여 그 이상인 예산요청에는 모두 상한액을 배정합니다. 
   상한액 이하의 예산요청에 대해서는 요청한 금액을 그대로 배정합니다. 

• 위 조건을 모두 만족하는 상한액을 구하라

  → 조건에 맞는 답이 여러 개 일 수 있고, 그 중 최대값

• 풀이

  1. 이분 탐색의 대상(범위) = 상한액

  2. 상한액의 최소 = 0 상한액의 최대 = 예산들 중 최대값

  3. 위 조건에 맞게 범위를 줄여나가며 탐색

  class Solution
  {
      public int solution(int[] budgets, int M)
      {
          int start = 0, end=0;
          for(int v:budgets){
              if(v > end) end = v;
          }
          while(start <= end)
          {
              int sum = 0;
              int mid = (start + end) / 2;
              for(int element : budgets)
                  sum = element > mid ? sum + mid : sum + element;
              if(sum > M) end = mid - 1;
              else start = mid+1;
          }
          return end;
      }
  }

 

 

🔗 프로그래머스, 입국심사

1. 처음에 모든 심사대는 비어있습니다. 
한 심사대에서는 동시에 한 명만 심사를 할 수 있습니다. 가장 앞에 서 있는 사람은 비어 있는 심사대로 가서 심사를 받을 수 있습니다. 

2. 하지만 더 빨리 끝나는 심사대가 있으면 기다렸다가 그곳으로 가서 심사를 받을 수도 있습니다.

• 모든 사람이 심사를 받는데 걸리는 시간을 최소로 만들고, 그 시간을 구하라

 

• 풀이

  1. 이분 탐색의 대상(범위) = 심사하는데 걸리는 시간

  2. 심사 시 최소 시간 = 0 심사 시 최대 시간 = 가장 오래 걸리는 심사대에서 모든 사람들이 심사를 할 경우

  3. 위 조건에 맞게 범위를 줄여나가며 탐색

  import java.util.Arrays;
  class Solution {
      public long solution(int n, int[] times) {
          Arrays.sort(times);
          long right = (long)times[times.length-1]*(long)n;
          long left = 0;
          long mid;
          while (left < right) {
              long done = 0;
              mid = (left + right)/2;
              for (int v : times) {
                  done += mid/v;
              }
              
              if (done < n) left = mid + 1;
              else right = mid;
          }
  
          return right;
      }
  }

 

 

---

⍞ Reference

• 나무위키, 이진탐색