계산 기하(computational geometry) 알고리즘이란,
점, 선, 다각형과 원 등 각종 기하학적 도형을 다루는 알고리즘이다.

2차원의 평면 도형과 3차원의 입체 도형을 모두 다루는 주제이지만 여기에서는 2차원 기하학만을 다룬다.

계산 기하 관련 코드 구현 시, 필수적 개념

벡터의구현

📜

방향과 거리를 모두 알고 있으면 두 점 사이의 상대적인 위치를 정확히 표시할 수 있다.
이러한 방향과 거리의 쌍을 벡터(vector)라고 한다.

벡터의 시작점을 바꿔도 벡터는 변하지 않기 때문에, 벡터의 시작점을 항상 좌표 공간의 원점으로 정한다.

벡터의 덧셈과 뺄셈

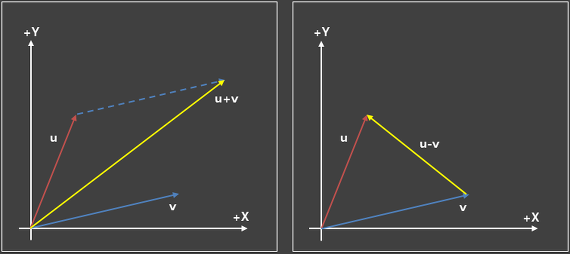
벡터의 대소 비교
- 끝점의 x 좌표가 작은 벡터 → 더 작은 벡터
- 끝점의 x 좌표가 같을 경우, y 좌표가 작은 벡터 → 더 작은 벡터

벡터의 극 각도(polar angle) 계산

💡

극 각도란, 해당 벡터의 방향이 x 축의 양의 방향으로부터 반시계 방향으로 얼마나 차이 나는지를 나타낸다.

(y, x) 좌표가 주어질 때 각 좌표의 부호를 이용해 자동으로 이 각도를 계산해 준다.
반환 값은 [-π, π] 이기 때문에, 여기서는 항상 이 각도를 [O, 2π) 안으로 보정하게끔 작성한다.
```
public double polar() {
	return Math.mod(Math.atan2(y, x) + 2*PI, 2*PI);
}
```

점과 직선, 선분의 표현

점 : 해당 접을 끝 점으로 갖는 벡터로 표현

선분 : 두 개의 끝 점을 두 개의 벡터로 표현

직선 : 직선에 포함된 임의의 선분을 이용해 표현

→ 이렇게 표현하는 것은 귀찮음.
But, 벡터를 기준으로 생각하는 것이 많은 경우 코드를 간결하게 하고 문제를 푸는 데 강력한 도구가 된다.

물론 이 책에서 사용하는 표현 방식이 항상 최선은 아니며,
중요한 것은 해당표현 방식을 프로그램 내에서 일관적으로 사용하며 여러 표현 방식을 섞어쓰지 않는 것이다.

벡터의 내적과 외적

기하학적인 의미를 가지고 있기 때문에 다양한 계산 기하 알고리즘을 구현하는 데 유용하게 사용된다.

벡터의 내적(inner product)

두 2차원 벡터 내적 a·b는 위와 같이 두가지 방법으로 계산할 수 있는 실수값이다.

내적을 통해 두 벡터 사이의 각도를 알 수 있다!

실제 내적을 계산할 때는 첫번째 식 사용

내적의 용도
- 벡터의 사이각 구하기
  
  → 가장 기초적인 용도
- 벡터의 직각 여부 확인하기
  
  (길이가 0이 아닌 두 벡터) a와 b의 내적이 0? = 두 벡터는 항상 직각!
  
  → cos𝜽 = 0 ? 𝜽 = π/2 혹은 𝜽 = π*3/2 이기 때문에
  
  < 장점 >
  1. 수행 속도가 느린 acos 함수를 호출하지 않아도 됨
  1. 수치적으로 훨씬 안정적
- 벡터의 사영(vector projection)
  
  💡
  
  a의 벡터 사영 = 벡터 b에 수직으로 빛이 내리쬘 때, 벡터 a가 b위에 드리우는 그림자
```
vector2 project(const vector2& rhs) const{
	vector2 r = rhs.normalize(); //단위 벡터로 바꿈으로써 코드가 훨씬 간단해짐
	return r*r.dot(*this);
}
```

벡터의 외적(cross product)

두 개의 3 차원 벡터에 대해 정의되는 연산으로, 3 차원 벡터 a, b가 주어졌을 때 이 두 벡터에 모두 수직인 다른 벡터를 반환한다

→ 3차원 벡터에서 z 좌표가 0 인 3차원 벡터로 생각하여 2차원 벡터를 정의할 수 있다.

외적에서 유용한 것은 반환되는 벡터의 길이와 방향이다.
2차원벡터 외적 axb 의 길이는 다음과 같이 두가지 방법으로 계산할 수 있다

외적의 용도
- 면적 계산하기
  
  외적의 절대값 = a, b를 두 변으로 하는 평행 사변형의 넓이
  
  → 원점과 a, b를 꼭지점으로 하는 삼각형 넓이의 정확히 두 배
  → 외적의 절대값을 구하고, 이를 반으로 나누어 해당 삼각형의 넓이를 구할 수 있음
  
  일반 다각형에도 확장이 가능하기 때문에 아주 유용!
- 두 벡터의 방향 판별
  
  sin-𝜽 = -sine𝜽
  
  → 외적이 음수인지 양수인지를 알면, 𝜽가 양수인지 음수인지 쉽게 알 수 있음.
  
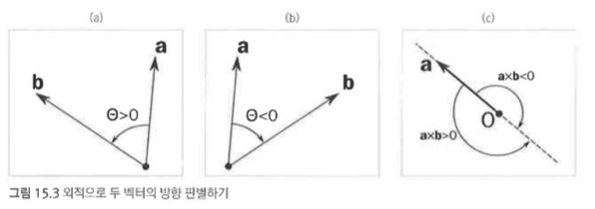
  두 벡터 a, b의 외적 a*b가
  1. 양수? b가 a로 부터 반시계 방향으로 180도 이내에 있음
  1. 음수? 시계 방향으로 180도 이내에 있음
  → 벡터의 극각도를 계산하는 polar()도 가능하지만 외적을 사용하는 것이 속도도 빠르고, 수치적으로 안정적이며, 코드도 간결하다.

교차와거리, 면적

직선과 직선의 교차

계산 기하 문제의 단골 주제. 예외 없이 동작하는 코드를 작성하는 것이 관건

가장 간단한 방법

→ 직선을 한 점과 방향 벡터, 즉 a+p·b 형태로 표현하는 것.
a+p·b와 c+q·d 의 교점을 구하기 위해서는 a+p·b=c+q·d 방정식을 풀면 된다.

선분과 선분의 교차

한 직선위에 두 선분이 있을 때 , 이 선분들의 관계는 넷 중 하나이다.

두 선분이 서로 겹치지 않음

3. 두 선분이 겹쳐짐

2. 두 선분이 한 점에서 닿음

4. 한 선분이 다른 선분 안에 포함됨

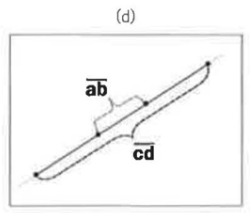
→ 벡터의 비교 함수 사용

→ a < p < b가 성립하면, p는 이 두 점을 잇는 선분 위에 있다.

선분과 선분의 교차: 교차점이 필요 없을 때

ccw( ）를 이용하면 이 조건들을 간단하게 확인할 수 있다.

ccw(a, b, c) * ccw(a, b, d) < 0

ccw(c, d, a) * ccw(c, d, b) < 0

→ 둘 중 하나는 항상 음수여야 하기 때문에

→ 벡터의 비교 함수 사용

→ a < b, c < d인 네 점 a, b, c, d가 일직선 상에 있을 경우 두 선분이 겹치지 않기 위해서는 b < c 혹은 d < a 여야한다.

점과 선 사이의 거리

직선 위에서 p와 가장 가까운 점 q = 벡터 p-a가 벡터 b-a에 내린 벡터 사영

→ 선분-선분 거리 계산에도 유용

자주 하는 실수와 유의점

퇴화 도형

'일반 위치(general position)'만 고려하지 마라.

💡

일반 위치란,
말 그대로 도형들의 상대적 위치의 일반적인 경우를 가리킴.

↔ 퇴화(degenerate) 도형

일직선 상에 있는 세 개 이상의 점들

서로 평행이거나 겹치는 직선/선분들

넓이가 0인 다각형들

다각형의 변들이 서로 겹치는 경우

직교 좌표계와 스크린 좌표계

두 가지의 다른 좌표계를 착각하지 마라.

다른 실수들

의외로 많은 기하 문제들은 정수만을 사용해 해결 가능하다.

삼각함수들은 느리고 수치적으로 불안정하므로 가능한 사용하지 마라.

acos(), asin()은 입력으로 ±1 범위의 실수만을 받아들인다. → 범위를 꼭 제한하는 습관을 들여라

sqrt함수 입력에 0 대신 아주 작은 음수가 들어가는 실수도 조심해라. → 범위 제한!

'정리 log > 책' 카테고리의 다른 글

[실무로 배우는 시스템 성능 최적화] 서버 모니터링 (0)	2020.09.06

lijly

[알고리즘 문제해결전략] 15. 계산 기하

계산 기하 관련 코드 구현 시, 필수적 개념

벡터의구현

점과 직선, 선분의 표현